Bayesian Inference
Bayesian inference is the key to making good decisions. It allows you to combine new information with previous information and beliefs in a balanced and principled manner.
Join Our Team
Classical statistical inference estimates unknown or uncertain parameters of a population from data sampled from that population. Bayesian inference improves this process by applying Bayes Rule to include prior information in making these estimates and guiding future decisions. This prior information can be obtained from previously received data or from knowledge obtained before the sampling begins.
3 Goals of Statistical Inference
Parameter estimation – estimating the values of a population’s parameters such as mean and standard deviation
Data prediction – using those parameters to develop statistical models that predict future data
Model comparison – deciding which statistical model provides the best fit to the data
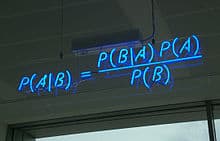
Bayesian vs. Classical Statistics
Bayesian statistics goes beyond the limitations of classical statistics by including prior information when estimating a parameter of interest. This information (aka the prior probability distribution) on the parameter can be based on both objective and subjective information. Classical statistics has no mechanism to include this prior information in a principled and consistent fashion. This limits the usefulness of classical statistics in areas where data is sparse. Bayesian inference allows statisticians to combine prior information with new data to update their estimates in a fashion that gives the proper balance between the old and the new. This enables the statistician to combine subjective information (expert opinion) with data in a principled fashion to improve estimation and decision making. We have successfully applied Bayesian techniques to develop methods search for lost ships, lost planes, lost cities, and lost people.
Practical Applications of Bayesian Inference
Problems involving decision-making in dynamic situations with high uncertainty are naturally and effectively tackled by Bayesian inference and decision theory. Metron has successfully applied this Bayesian approach to develop software for Coast Guard search and rescue personnel to plan a search for someone lost at sea. Bayesian inference allows us to make the best decision we can given all the information, both subjective and objective, available at the time.
References
Featured Project: Lobsterman Overboard
“Search and Rescue Optimal Planning System” by T.M. Kratzke, L.D. Stone, and J.R. Frost, in Proceedings of the 13th International Conference on Information Fusion (Fusion 2010), Edinburgh, Scotland 26-29 July 2010
“Man Overboard” by P. Tough, New York Times Magazine 5 January 2014
“Search for the Wreckage of Air France AF447” by L.D. Stone, C.M. Keller, T.M. Kratzke, and J.P. Strumpfer, Statistical Science (2014) Vol 29 pp 69-80
”Search for SS Central America: mathematical treasure hunting” by L.D. Stone, Interfaces (1992) Vol 22 pp 32-54
Related Content
Advanced Data Exploitation
Sometimes data is easy to interpret, but more often the narrative is hidden in the noise. Advanced data exploitation uses statistical techniques and domain knowledge to help data tell its story.
Explore Advanced Data Exploitation
Machine Learning – AI
Machine learning is a branch of artificial intelligence in which machines learn to perform tasks by processing data. These tasks include making predictions, clustering similar data, and taking action.
Explore Machine Learning – AI
Network Science
Network science explores the results of connection. Whether it’s people, objects, or even ideas – network science untangles the complexities of large systems of any kind of connectable thing.
Explore Network Science
Trend Analysis and Anomaly Detection
Trend analysis models normalcy as it changes over time. Normalcy models are used predict the future and identify anomalous new or past events.
Explore Trend Analysis and Anomaly Detection
Metron Careers
Data Science Career Opportunities
Metron hires data scientists with experience researching novel approaches that advance the state of the art. Our data scientists apply these innovations to new problem domains working alongside subject matter experts. They are familiar with machine learning tools and pipelines and work with software engineers to integrate solutions into client systems.