Nonlinear Gradient Descent Methods
Metron scientists use nonlinear gradient descent methods to find optimal solutions to complex resource allocation problems and train neural networks.
Join Our Team
Optimization can lead to savings in time, reduction in computational costs, as well as helping discover solutions to complex mechanical, resource allocation and positioning, and machine learning problems.
Nonlinear Gradient Descent
Nonlinear gradient descent methods are one type of optimization tool useful for finding the minimum (or maximum) value of a function. They involve taking a sequence of steps, each of which generally moves in the direction of steepest decrease of the function. Metron data scientists have applied nonlinear gradient descent to a wide range of problems from positioning of mobile assets to satisfy a joint goal, training deep neural networks, and solving joint control strategies for mechanical systems.
References
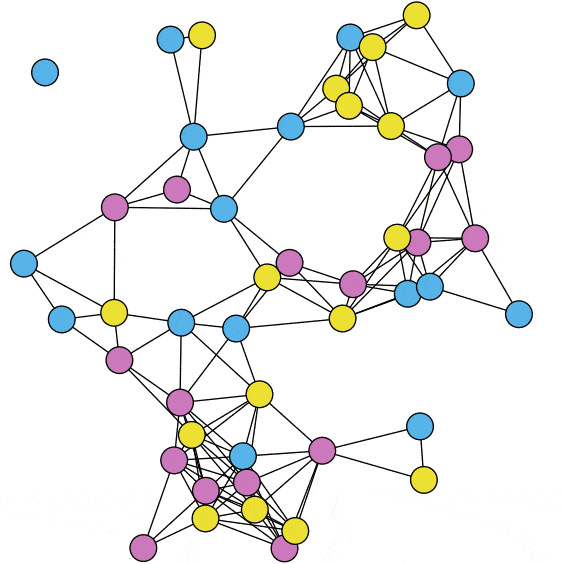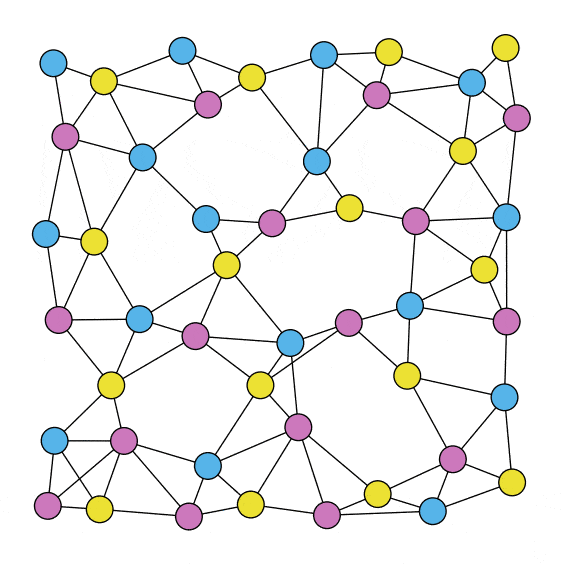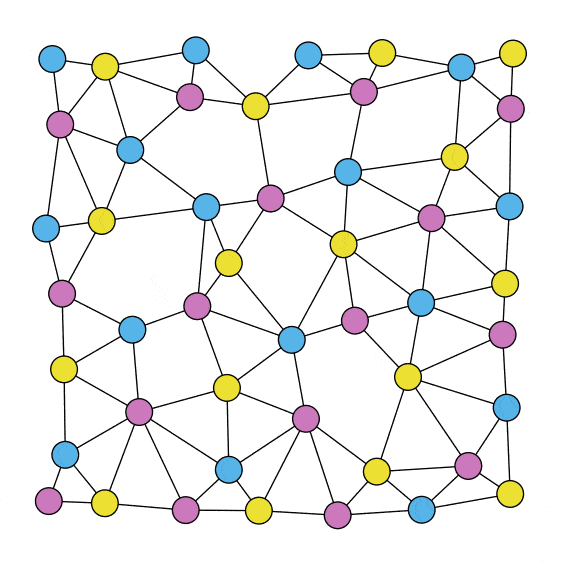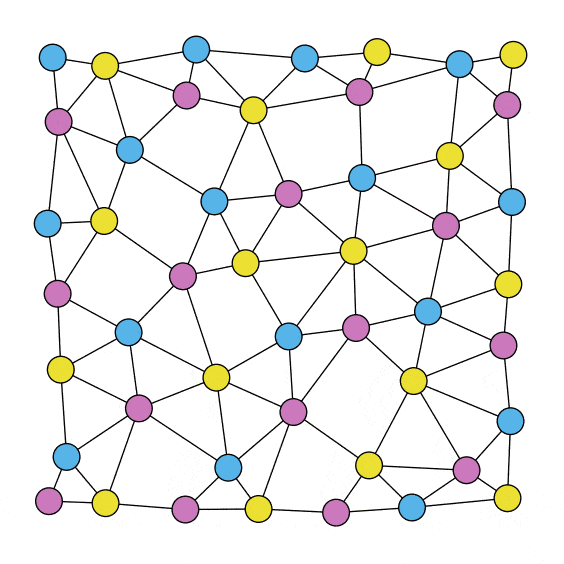
Nonlinear Gradient Descent is used to find the optimal position for each element.
Related Content
Bayesian Optimization
Bayesian optimization is a cost-effective method for solving "black box" function-optimization problems in machine learning by strategically choosing a highly informative set of points to sample.
Explore Bayesian Optimization
Metaheuristics
Metron applies advances in artificial intelligence to reduce the computational cost required for searching complex solution spaces.
Explore Metaheuristics
Reinforcement Learning
Reinforcement learning uses trial and error feedback to teach machines how to achieve a goal. Metron develops AI systems that teach themselves.
Explore Reinforcement Learning
Stochastic Dynamic Programming
Metron data scientists apply stochastic dynamic programming methods to solve incredibly large and complex planning problems.
Explore Stochastic Dynamic Programming
System of Systems
Metron is a pioneer in advanced decision aid technologies for composing systems of systems and mission plans.
Explore System of Systems
Metron Careers
Decision Support Career Opportunities
Metron hires research scientists with experience developing novel approaches that advance the state of the art in mathematics and artificial intelligence. Our scientists work alongside subject matter experts applying these innovations to new problem domains.